Introduction: Exploring Physics Measurements
Physics is the study of natural sciences, encompassing matter, motion behavior through time and space, and related concepts such as energy and force. At its core, physics relies on precise quantification, and that’s where “Physics measurements” come into play.
In this exploration of physics fundamentals, we delve into two key categories: scalar and vector quantities. These measurements serve as the bedrock of our understanding of the physical world, helping us navigate complex phenomena and solve real-world problems.
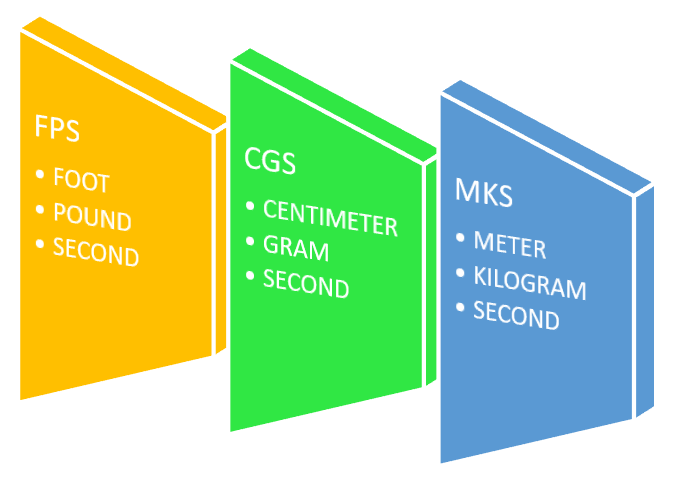
MKS System (Meter-Kilogram-Second System)
The MKS system, short for Meter-Kilogram-Second system, is a fundamental system of units used in physics measurements. In this system, the basic units of measurement are as follows:
- Length (L): Meter (m)
- Mass (M): Kilogram (kg)
- Time (T): Second (s)
The MKS system is widely adopted for its simplicity and compatibility with the International System of Units (SI). It forms the basis for many physical measurements, allowing scientists and engineers to quantify various physical phenomena accurately.
FPS System (Foot-Pound-Second System)
The FPS system, or Foot-Pound-Second system, is another historical system of units used in physics measurements. In this system, the basic units of measurement are as follows:
- Length (L): Foot (f)
- Mass (M): Pound (p)
- Time (T): Second (s)
While the FPS system has been largely replaced by the MKS and SI systems due to their international standardization, it played a crucial role in the history of physics measurements, particularly in English-speaking regions.
CGS System (Centimeter-Gram-Second System)
The CGS system, short for Centimeter-Gram-Second system, is yet another system of units used in physics measurements. In this system, the basic units of measurement are as follows:
- Length (L): Centimeter (cm)
- Mass (M): Gram (g)
- Time (T): Second (s)
The CGS system was historically used in various scientific disciplines, including electromagnetism and thermodynamics. However, like the FPS system, it has largely been supplanted by the MKS and SI systems in modern scientific research and engineering.
These systems of units, including MKS, FPS, and CGS, have played significant roles in the history of physics measurements. While the MKS system, with its meter-kilogram-second units, is the most prevalent and widely accepted in contemporary scientific research, understanding the historical context of FPS and CGS systems is essential for appreciating the development of physics measurements over time.
Physics Measurements – Quantities
Scalar: A scalar is a physical quantity described by a single element of a number field, typically a real number, often accompanied by units of measurement. Scalars possess only magnitude and lack direction. Examples of scalars include speed and mass.
Vector: On the other hand, a vector is a physical quantity characterized by both magnitude and direction, which are independent of each other. Vectors are often represented mathematically and geometrically. Examples of vectors encompass momentum, force, and velocity.
Types of Measurements: In physics, the fundamental parameters used for measurement are length, mass, and time. The international units and measurements organization introduced the S.I. (International System of Units) system in the 11th meeting in 1960, standardizing measurements worldwide.
Quantities are two types’ derived quantities and fundamental quantities.
Fundamental quantities are length, mass, time, temperature, electric current, luminous intensity and amount of substance.
Physical Quantities Mesaurement units and Their symbols
| SNo | Type | Fundamental Quantities | ||
| Length (L) | Mass (M) | Time(S) | ||
| 1 | F.P.S | Foot (f) | Pound (p) | Second(s) |
| 2 | C.G.S | Centi Meter (cm) | Gram (g) | Second(s) |
| 3 | M.K.S | Meter (m) | Kilo Gram (kg) | Second(s) |
Physics Measurements
Here’s a summary of fundamental quantities:
Fundamental Quantities:
- Length (L): Meter (m)
- Mass (M): Kilo gram (kg)
- Time (T): Second (s)
These fundamental quantities form the basis for measurements across various systems, including F.P.S (Foot, Pound, Second), C.G.S (Centimeter, Gram, Second), and M.K.S (Meter, Kilo Gram, Second).
Supplementary Quantities:
- Plane Angle: Radian (rad)
- Solid Angle: Steradian (sr)
Physical Quantities Measurement Units and Their Symbols:
- Length: Meter (m)
- Mass: Kilo gram (kg)
- Time: Second (s)
- Electric Current: Ampere (A)
- Temperature: Kelvin (K)
- Luminous Intensity: Candela (cd)
- Amount of Substance: Mole (mol)
| Physical Quantity | Units | Symbol |
| Fundamental Quantities | ||
| Length | meter | m |
| Mass | Kilo gram | kg |
| Time | Second | s |
| Electric Curent | Ampere | A |
| Temperature | Kelvin | K |
| Luminous Intensity | Candela | cd |
| Amount of Substance | mole | mol |
| Supplementary Quantities | ||
| Plane angle | radian | rad |
| Solid Angle | Steradian | sr |
Time: Time is a continuous, measurable quantity in which events occur in a sequence proceeding from the past through the present to the future. Time is a scalar quantity because it has no direction. Time in physics is defined by its measurement: time is what a clock reads.
Time is a component quantity of various measurements used to sequence events, to compare the duration of events or the intervals between them, and to quantify rates of change of quantities in material reality or in conscious experience.
One standard second is defined as the time taken for 9,192,631,770 periods of the radiation corresponding to unperturbed transition between hyperfine levels of the round state of cesium-133 atom. Atomic clocks are based on this. In atomic clocks, an error of one second occurs only in 5000 years. These clocks are very accurate, with a cesium atomic clock at the National Physical Laboratory (NPL) in New Delhi being used to maintain the Indian standard of time.
Meter: It is a unit for measuring length and distances. The meter was intended to equal 10-7 or one ten-millionth of the length of the meridian through Paris from pole to the equator. The meter is the length of the path traveled by light in a vacuum during a time interval of 1/299,792,458 of a second. The molecules in krypton (36Kr86) release energy when traveling from the 2p10 state to 5d5, and its wave rhythm equals 1,650,763.73 times.
Kilogram: It is the unit for mass, equivalent to the platinum and iridium mixture kept at Sèvres near Paris by the International Bureau of Weights and Measures.
Ampere: The ampere is the constant current that, when flowing through two straight parallel infinitely long conductors of negligible cross-section and placed one meter apart in a vacuum, would produce a force of 2 × 10-7 newton per unit length of the conductors.
Kelvin: This is the unit for measuring temperature, defined as 1/273 of the thermodynamic temperature of the triple point of water. The triple point of water is the temperature at which saturated water vapor, pure water, and melting ice coexist in equilibrium.
Candela: The candela measures light intensity. It is the luminous intensity in a given direction due to a source emitting monochromatic radiation of frequency 540 x 1012 Hz, with a radiant intensity of 1/683 watt per steradian.
Mole: The mole represents the amount of substance containing as many elementary entities as there are atoms in 0.012 kg of carbon-12.
Radian: A radian is the measurement for angle, equal to the angle between a sector with a length of radius and the center of a circle. 2π radians are equivalent to 360 degrees. Thus, 1 radian = 360° / 2π ≈ 57.17 degrees.
Dimension Formula: In physics, every quantity is associated with basic fundamental quantities such as mass (M), length (L), and time (T). The derived quantity expresses in basic fundamental quantities is called the dimensional formula. The dimension of a physical quantity is defined as the power to which the fundamental quantities are raised to express the physical quantity. The dimension of mass, length, and time is represented as [M], [L], and [T], respectively.
An equation containing physical quantities with dimensional formulas is known as a dimensional equation. Dimensional equations are obtained by equating dimensional formulas on the right and left-hand sides of an equation.
Example: To find the dimensional formula for Area, use the formula: Area = length x breadth. Since both length and breadth are expressed using the fundamental quantity length (L), the area’s dimensional formula is [L2].
Derived Quantities and Their Dimensional Formulas Table:
| Physical Quantity or Derived Quantity | Expression | Dimensional Formula |
| Area | Length x Breadth | [L2] |
| Density | Mass /Volume | [ML-3] |
| Acceleration | Velocity / Time | [LT-2] |
| Momentum | Mass x Velocity | [MLT-1] |
| Force | Mass x Acceleration | [MLT-2] |
| Work | Force X Distance | [ML2T-2] |
| Power | Work / Time | [ML2T-3] |
| Energy | Work | [ML2T-2] |
| Impulse | Force x Time | [MLT-1] |
| Radius | Distance | [L] |
| Pressure | Force / Area | [ML-1T-2] |
| Surface Tension | Force / Length | [MT-2] |
| Frequency | 1 / Time Period | [T-1] |
| Tension | Force | [MLT-2] |
| Torque | Force x Distance | [ML2T-2] |
| Angular Velocity | Angular Displacement / Time | [T-1] |
| Stress | Force / Area | [ML-1T-2] |
| Stress | Force / Area | [ML-1T-2] |
| Heat | Energy | [ML2T-2] |
| Heat Capacity | Heat Energy / Temperature | [ML2T-2K-1] |
| Charge | Current x Time | [AT] |
| Magnetic Induction | Force / (Current x length) | [MT-2A-1] |
| Faraday Constant | Avagadro constant X elementary charge | [ATmol-1] |

