Heap Sort is a powerful sorting algorithm that has earned a stellar reputation in the world of computer science. It’s known for its efficiency and reliability when it comes to sorting data. In this comprehensive guide, we’ll dive deep into Heap Sort, exploring how it works, its time and space complexity, and its real-world applications.
Understanding Heap Sort
Heap Sort is an improvement upon the Selection Sort algorithm. It operates by dividing the elements into two distinct regions: the sorted region and the unsorted region. The primary goal is to iteratively shrink the unsorted region by selecting the largest (or smallest) elements and moving them into the sorted region.
Historical Background of Heap Sort
Heap Sort was first introduced by J. W. J. Williams in 1964. Since then, it has become a fundamental sorting technique in computer science and is widely used in various applications.
How Heap Sort Works
The key to Heap Sort’s efficiency lies in its data structure: the heap. This binary tree structure ensures that the largest element (in the case of a Max heap) or the smallest element (in the case of a Min heap) is always at the top position of the tree.
The process of Heap Sort can be summarized as follows:
- Start with an unsorted list of elements.
- Create a Heap data structure, which can be a Max heap or a Min heap, from the list.
- Once the heap is successfully constructed, the top element of the heap is moved to an array.
- Reconstruct the heap with the remaining elements and select the top element again, placing it in the array.
- Repeat these steps until the entire list is sorted in the array.
Heap : A sorting algorithm that works by first organizing the data to be sorted into a special type of binary tree called heap. The heap itself consists of largest element at the top position of the tree.
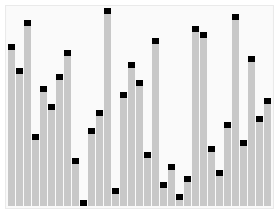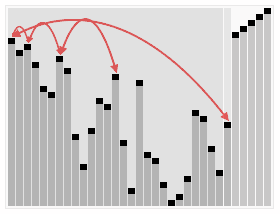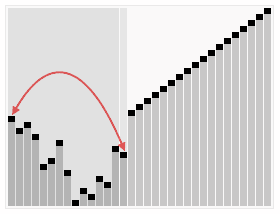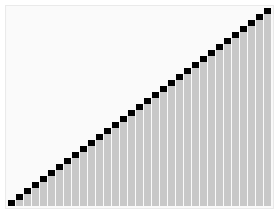
Working of Heap sorting: In the first step receiving an un sorted list and it create a Heap data structure (Max, Min heap). Once successfully built the heap, the first element of the heap may be either largest or smallest it depends on Max or Min heap, so put this heap into an array. Then we again make heap using the remaining elements, to again pick the first element of the heap and put it into the array. We keep on doing the same repeatedly until we have the complete sorted list in our array.
Time Compelxity of Heap Sort
Worst Case Time Complexity : O(n log n)
Best Case Time Complexity : O(n log n)
Average Time Complexity : O(n log n)
Space Complexity : O(1)
Furthermore, Heap Sort is space-efficient, with a space complexity of O(1). This means it requires a constant amount of additional memory, making it suitable for sorting large datasets.
Applications of Heap Sort
Heap Sort’s efficiency and low space requirements make it valuable in many real-world applications. Some common use cases include:
- Sorting large databases.
- Implementing priority queues.
- Operating system scheduling algorithms.
- Network routing algorithms.
In conclusion, Heap Sort is a 5-star sorting algorithm known for its speed, reliability, and versatility. Its ability to handle large datasets efficiently makes it a popular choice among developers and computer scientists. Whether you’re working with extensive databases or need to implement priority queues, Heap Sort is a trusty companion in the world of algorithms.
Heap sort is widely used sorting, and it requires a constant space for sorting a list. It is a not stable sort.
See the below Heap Sort example program in Java:
public class HeapSort
{
private static int[] a;
private static int n;
private static int left;
private static int right;
private static int largest;
public static void buildheap(int []a){
n=a.length-1;
for(int i=n/2;i>=0;i--){
maxheap(a,i);
}
}
public static void maxheap(int[] a, int i){
left=2*i;
right=2*i+1;
if(left <= n && a[left] > a[i]){
largest=left;
}
else{
largest=i;
}
if(right <= n && a[right] > a[largest]){
largest=right;
}
if(largest!=i){
exchange(i,largest);
maxheap(a, largest);
}
}
public static void exchange(int i, int j){
int t=a[i];
a[i]=a[j];
a[j]=t;
}
public static void sort(int []a0){
a=a0;
buildheap(a);
for(int i=n;i>0;i--){
exchange(0, i);
n=n-1;
maxheap(a, 0);
}
}
public static void main(String[] args) {
int []a1={6, 5, 3, 1, 8, 7, 2, 4};
sort(a1);
for(int i=0;i<a1.length;i++){
System.out.print(a1[i] + " ");
}
}
}
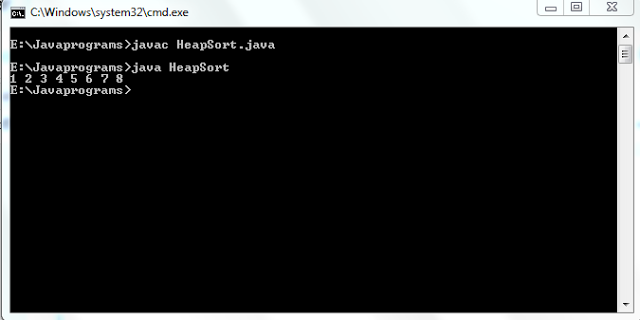
To run the above program save this as HeapSort.java
E:\Javaprograms>javac HeapSort.java
E:\Javaprograms>java HeapSort
1 2 3 4 5 6 7 8